William Chuang
Graduate Student, University of Arizona

E-mail: williamchuang@arizona.edu
Pronouns: he/him
I enjoy hiking and painting (including oil painting), and I am also deeply curious about neuroscience, psychology, and classical studies. I am particularly fascinated by innovative strategies for designing and coding neural network models—especially those that can recursively design, implement, and train new, evolved networks based on a parent model’s best configuration. In addition, I love exploring how, when, and what we learn to accomplish a chosen mission along all possible paths, ultimately working toward a comprehensive “user manual” for the human mind.
I have curated a selection of notes and resources to support
preparation for qualifying exams. These materials reflect some of my
approaches to key topics and problem-solving strategies. They are
available for review in the following Google Drive folder:
Access my Qualifying Exam Notes
Additionally, here is my YouTube channel, where I plan to share worked-through math problems regularly: @william_chuang
You can find some of my older math notes here:
My old notes
More About Me Before 2015
Detailed Records Prior to 2014
The Genealogy of the Chuang Family (also spelled Cheung, Chong, etc.)
According to statistics from the U.S. Census Bureau, there are an estimated 2,931 individuals in the United States with the surname Chuang, ranking it 11,621st in prevalence, at 0.92 per 100,000 people. In East Asia, the name Chuang remains relatively rare; it ranks 323rd in the Song Dynasty’s “Hundred Surnames.” As a result, many individuals with the surname Chuang are unfamiliar with their lineage beyond three generations and may even feel like outsiders to the larger clan.
Historical data indicates that fewer than 50,000 people (around 0.06% of the total population) bore the surname Chuang during the Song Dynasty, with Fujian hosting the highest concentration. By the Ming Dynasty, approximately 120,000 people (about 0.12% of the total population) carried this surname. Today, the name is most commonly found in Guangdong, Fujian, Taiwan, Jiangsu, Zhejiang, Shandong, Heilongjiang, Jilin, Shanghai, and Liaoning.
My mother was born in Wucuo (now Erlun) in Yunlin County, and my father was born in Erlin Township—once known as Gielem (a region known for deer) to the Dutch. I was born in New Taipei City, Taiwan, in 1988. Based on my grandparents’ family records, I am the 20th generation of the Chuang family to settle in Taiwan after our ancestors first arrived in the 1600s, following the Dutch occupation. This migration reminds me of the Mayflower pilgrims who arrived in the Americas around the same time—my ancestors similarly ventured forth in pursuit of freedom and opportunity.
A more recent notable figure in the Chuang family is Zhuang Yunkuan (also known as Yunkuan Chuang), who served as both a Qing Dynasty and Republic of China politician, as well as a Chinese calligrapher. He was a delegate in drafting the Republic of China’s provisional constitution and, in 1925, joined the board of directors of the National Palace Museum.
There is also a branch of the Chuang family in Guangdong and Hong Kong. Among its most well-known members are Cheung Jing-on, his daughter Chong Yuet-ming, and his nephew.
Advancing Transformer Efficiency Through Dynamic Scaling Factors: My Research Journey
Introduction
The transformer architecture has revolutionized deep learning, powering state-of-the-art large language models (LLMs) such as GPT-4. However, the reliance on brute computational power to scale these models presents significant challenges, including high costs and inefficiency. My research focuses on dynamically optimizing the scaling factor \(\beta\) in transformers to improve efficiency and accuracy. This journey has been both challenging and rewarding, and I am proud to share the progress I have made.
Timeline and Research Progress
Early Encounters with the Ising Model
- In 2008, I implemented my first Ising model code in a computational physics course using Fortran 99, taught by Dr. Chi-Ning Chen at NDHU. This experience introduced me to computational techniques in statistical physics and laid the foundation for my later studies of the model.
-
Around the same time, I also conducted an experiment as part of my second-year physics mandatory course at NDHU, which demonstrated the phenomenon of critical opalescence. The experiment, using a freon substance with a critical temperature of about 80°C, involved observing the liquid-vapor interface at the critical point. The system became milky, with liquid droplets and vapor bubbles scattering light as they reached a critical equilibrium.
Video | DOI
This experiment, in which the system transitions through critical points, inspired me to model the training of deep neural networks in terms of phase transitions. Just as the system reaches an equilibrium state at the critical point, deep learning models can achieve peak efficiency as the loss function converges. Starting near these critical point conditions can significantly reduce the training cost, offering an interesting analogy between the physical and computational worlds.
Additionally, since we are using neural networks to model nature and the universe, this approach can also be applied in the reverse direction, modeling deep neural networks through physical world examples. - Later, in my graduate course Statistical Mechanics II at NTU, taught by Dr. Ning-Ning Pang, I had the opportunity to present my final project as an independent study in May 2012. In this presentation, I studied the known solutions of the Ising model as introduced in T.D. Lee’s lecture notes (Statistical Mechanics). After reading it, I found that these solutions might have a profound connection to the Riemann zeta function in number theory or complex analysis, which became the focus of my independent study.
-
Reflecting on this work, I find Charles M. Newman's 2016 minicourse to be a particularly articulate exploration of the interplay between analytic number theory and statistical mechanics. While my presentation predated this minicourse, his insights provide a valuable modern perspective on these connections. The abstract of his lectures can be found
here,
and the full lectures are available on YouTube:
- Following this, I further explored the Ising model and its broader implications through various perspectives. I engaged with key references, including David Tong's lectures on Statistical Field Theory, Paul Ginsparg's Applied Conformal Field Theory, and Kerson Huang's Statistical Mechanics course at NTU.
- Furthermore, I studied Landau's and Feynman's approaches to statistical mechanics, which provided deeper insights into the underlying mathematical structures. My independent study with Dr. Heng-Yu Chen at NTU further solidified my understanding, particularly in the context of field-theoretic methods and their applications to statistical physics.
- During my Intro to CS course at USF in 2015, I discussed with Dr. Cindi Thompson how the Ising model could be used to explain deep learning neural networks during her office hours. At that time, we also read and shared about three or four research papers on this topic.
- Additionally, after reviewing the online lectures of Chuck Newman, as recommended by Prof. Sunder Sethuraman, I worte three notes that further explore these connections in detail:
December 2022 – January 2023
- Began investigating the role of the scaling factor \(\beta\) in self-attention mechanisms.
- Developed theoretical foundations inspired by statistical mechanics and optimization theory to dynamically adjust \(\beta\).
September 2023
- Drafted the first version of my research paper, focusing on the theoretical basis and moderate empirical results to maintain credibility while avoiding overstatements.
December 2023
- RTG Presentation: Presented a preliminary version of my work at the RTG seminar at the University of Arizona.
- The presentation focused on moderate improvements in model performance by dynamically optimizing \(\beta\).
- Received mixed feedback, with some skepticism due to the lack of large-scale demonstrations.
October 30, 2024
- Export Office Rejection:
- Contacted the Export Control Office at the University of Arizona to ensure compliance with dual-use regulations.
- Despite explaining the potential dual-use nature of my work, the export office declined to classify it as significant or requiring clearance.
- Their Response: "We do not need to clear your work on any of the projects you have described."
- Impact: This rejection reflected a lack of institutional recognition of the potential importance of my work for U.S. competitiveness and national security.
-

Portion of the description I wrote. 
Last email I received from the Export Control Office.
December 2024
- Published the work on ResearchGate to ensure accessibility and transparency. While ResearchGate has a smaller reach than arXiv, it allowed me to share my results with the academic community.
January 2025
- Preparing further refinements to the paper, incorporating additional experimental results and practical implications to submit to alternative venues.
Key Contributions
-
Dynamic Scaling Factor Optimization:
- Proposed a dynamic adjustment to the traditional scaling factor (\(\beta = \frac{1}{\sqrt{d_k}}\)) used in transformers.
- Demonstrated that a dynamically optimized \(\beta\) significantly improves test accuracy across various datasets and model configurations.
- Published moderate results showing substantial improvements over traditional methods without overstating claims.
-
Experimental Results:
- The results showcase consistent improvements in accuracy when using the dynamic scaling factor compared to the traditional fixed method.
- Key findings include accuracy improvements across varying categories, sequence lengths, and training set sizes.
-
Theoretical Foundation:
- Derived the dynamic scaling factor optimization method based on insights from statistical mechanics and energy minimization principles.
- Demonstrated the theoretical soundness of the method in reducing redundancy and enhancing efficiency in self-attention mechanisms.
Landau’s 1940 Preface
Theoretical Physics Course · Mechanics
As everyone knows, physics consists of two main disciplines: experimental physics and theoretical physics. The large number of physical laws we know can be derived from a small number of very general principles. Such derivation, and the establishment of those general principles, call for a distinctive method, and this method defines a particular branch of study—namely, theoretical physics.
Theoretical physics uses mathematical tools and methods to arrive at its own results and conclusions. However, theoretical physics differs fundamentally from mathematics in that it has a direct link to experimental results. This is not to suggest that the most general laws can only be built on experimental data, nor that drawing conclusions from those laws does not also require prior experimental investigations. Without such investigations, one cannot judge which among the many interwoven factors are important or negligible. Once the relative importance of these factors is known, the essential task of theoretical physics is essentially complete. Further application of these equations to specific cases of varying complexity soon becomes a matter of purely mathematical study, forming what we call “mathematical physics.”
The goal of theoretical physics is to establish physical laws, that is, to establish relationships among physical quantities. Determining the specific numerical values of those quantities is generally not the task of theoretical physics, since, for numerical issues, experimental methods are often simpler and do not require labor-intensive calculations. Naturally, if a situation is simple enough, theory can directly compute the numerical values.
It must be emphasized that theoretical physics aims to establish and characterize the relationships between the physical quantities of a given phenomenon. Consequently, one can only devise a proper theory if such relationships truly exist in nature. Yet in many cases, the physical quantities of interest bear no relation to each other at all; in other words, they belong to entirely separate categories in different natural phenomena. Hence, in certain situations, the absence of a dedicated theory does not imply an inability to explain that phenomenon; if the most general laws can yield the same result, there is no necessity for a specialized theory.
Approximate analysis plays a tremendous role in theoretical physics. First, every “exact” law is in reality approximate, because in the vast majority of cases, that approximation offers sufficient accuracy. Second, theoretical physics does not strictly demand absolute accuracy in physical laws. If one defines the scope of a given phenomenon in advance, it suffices for the outcome to meet the required degree of precision. That is why we can still use Newtonian mechanics for analyzing the trajectory of artillery shells, despite knowing it is not absolutely accurate, simply because it is sufficiently precise in that domain, and we turn to relativity only when necessary for higher accuracy.
For this reason, in theoretical physics, there coexist certain theories (often referred to as “classical theories”) that have been shown to be less accurate alongside those that are more exact. They remain useful because, within certain specific ranges of phenomena, they retain their applicability. Any logically complete theory, once verified as valid within a certain accuracy range, does not lose its value. Indeed, partial or approximate results, derived in particular cases, remain embedded in any subsequent, more precise theory. Plainly, this category also includes those still under development or not yet fully coherent; they, too, have significance in the progression of theoretical physics.
Thus, we see that a key process in general physical theory lies in deducing more specific laws from the most general principles, without neglecting the central role of careful consideration of the most important factors. Overlooking those primary factors while relying solely on coarse simplifications can lead to ignoring the true scale or magnitude of the phenomena. In reality, the forms of phenomena themselves are often approximate, and the functional relationships among the physical quantities that describe them are similarly approximations. When studied at higher levels of precision, these relationships may reveal deeper meanings.
Determining the level of approximation at which one examines a phenomenon is exceptionally important in theoretical research. The gravest error is to adopt an extremely precise theory and exhaustively compute every subtle correction, while failing to recognize the broader advantages that a more streamlined or holistic approach might offer.
L. D. Landau
1940
(Note: Landau wrote this preface in 1940, when computational tools were very limited, so numerical experiments remained challenging.)
Relevance of Landau’s 1940 Preface to My Research
I find Landau’s perspective in his 1940 Preface to Theoretical Physics Course particularly resonant with the challenges in large-scale machine learning today. My academic path, spanning mathematics, physics, and computer science, allows me to appreciate how Landau’s emphasis on identifying key parameters and simplifying complex systems parallels the efficient training of transformer architectures. His insight—that theory provides a guiding framework but requires the isolation and rigorous examination of the most critical factors to achieve practical, approximate solutions—is especially relevant to machine learning, where computational resources are finite and model complexity can be immense.
Specifically, Landau’s discussion about leveraging general principles to sift out essential elements is deeply relevant to the “scaling factor,” or “temperature parameter,” often denoted by β, in transformer-based self-attention. Much like Landau’s insistence on identifying the key parameters governing physical phenomena, a dynamically optimized β pinpoints the core drivers of attention mechanism performance. Rather than devoting overwhelming computational effort to brute-force hyperparameter tuning, the principle of focusing on the most significant contributing factors—echoing Landau’s approach—yields both conceptual clarity and practical efficiency in modern AI models.
In the context of transformers, the traditional scaling factor \( \beta = \frac{1}{\sqrt{d_k}} \), introduced in Attention is All You Need, is treated as a fundamental parameter for ensuring stable self-attention dynamics. However, Landau’s perspective challenges us to question whether such heuristics truly reflect the underlying physics or mathematics of the system. If we consider the established equivalence between deep neural networks and spin-glass models, as demonstrated in LeCun’s seminal work on loss landscapes, the role of \( \beta \) becomes analogous to the inverse temperature in the Ising model—a parameter deeply tied to criticality and phase transitions. Could it be that this choice of \( \beta \) oversimplifies the dynamics of transformers and N-dim Ising models, ignoring subtleties that a more rigorous, theoretically grounded approach might uncover?
By leveraging the mathematical connections between Ising models, statistical mechanics, and deep learning, I argue that a dynamic optimization of \( \beta \), informed by principles from energy minimization and criticality, offers a pathway to more efficient and scalable transformer architectures. This approach not only aligns with Landau’s methodological rigor but also holds the potential to address long-standing challenges in both machine learning and statistical physics, such as solving N-dimensional Ising-like problems. I invite the broader academic and machine learning communities to explore these connections further, using well-established mathematics to refine hyperparameter selection and advance the field.
Finally, in the same way Landau accentuates the intimate relationship between theoretical foundations and experimental verification, my research underscores that the best outcomes come from bridging foundational theory with empirical tuning. I capitalize on the dynamic nature of \( \beta \)—rooted in statistical mechanics and energy minimization—to guide real-time updates of the self-attention process. This holistic cycle of theory informing practice, and vice versa, illustrates precisely why Landau’s arguments still hold tremendous value today: when major parameters are systematically refined based on a sound theoretical framework, significant leaps in performance and efficiency can be realized.
Connecting the Ising Model to Deep Learning and Transformers
The mathematical and theoretical connections between the Ising model, spin-glass systems, and modern deep learning architectures like transformers have been well-studied. The following notable works highlight these connections, providing a foundation for understanding the equivalence or similarity between these systems:
Key Papers and Abstracts
-
"The Loss Surfaces of Multilayer Networks" (2015)
Authors: Anna Choromanska, Mikael Henaff, Yann LeCun, et al.
This foundational paper investigates the landscape of loss surfaces in deep neural networks, using tools from statistical physics. The authors demonstrate that the structure of loss surfaces in multilayer networks can be analyzed through connections to the energy landscapes of spin-glass models, such as the Ising model. This work establishes theoretical parallels between deep learning and statistical mechanics, providing insights into why neural networks are able to find good minima despite the complexity of their loss surfaces.
Read the Paper -
"Deep Learning the Ising Model Near Criticality" (2017)
Authors: Alan Morningstar and Roger G. Melko
This study investigates the capability of deep generative models, such as Deep Boltzmann Machines and Deep Belief Networks, to learn the probability distribution of a two-dimensional Ising system. The authors compare these deep architectures to shallow networks like Restricted Boltzmann Machines, focusing on their accuracy in generating energetic observables near the phase transition.
Read the Paper -
"Explaining the Machine Learning Solution of the Ising Model" (2023)
This paper shows how a neural network without hidden layers can determine the critical temperature of the ferromagnetic Ising model's phase transition. The study provides insights into the strategies employed by neural networks in solving such problems, paving the way for explainable machine learning applications in physics.
Read the Paper -
"Ising Models of Deep Neural Networks" (2022)
Authors: Dusan Stosic, Darko Stosic, Borko Stosic
The authors map deep neural networks to classical Ising spin models, allowing for a description using statistical thermodynamics. The study reveals that well-trained networks exhibit structures in their weights that span a wider range of realizable energies compared to poorly trained ones.
Read the Paper -
"Inverse Ising Inference by Combining Ornstein-Zernike Theory with Deep Learning" (2017)
This research establishes an analogy between the inverse Ising problem and the Ornstein-Zernike formalism in liquid state physics. A deep neural network is employed to learn closure relations from Ising model simulations, outperforming traditional methods in inferring generative models from data.
Read the Paper -
"A Deep Dive into the Connections Between the Renormalization Group and Deep Learning in the Ising Model" (2023)
Author: Kelsie Taylor
This paper examines parallels between unsupervised deep learning and renormalization group flow through the lens of the two-dimensional Ising model. Restricted Boltzmann Machines are used to explore whether deep learning can be interpreted as a layer-by-layer coarse-graining process akin to renormalization.
Read the Paper
Questioning the Validity of Traditional β in Transformers
Inspired by the works above, particularly LeCun's analysis of loss landscapes in deep networks, consider this reasoning:
- Transformers, like deep neural networks, share mathematical similarities with Ising models or spin-glass systems, as evidenced by LeCun's work and others.
- The traditional scaling factor \( \beta = \frac{1}{\sqrt{d_k}} \), used in transformer self-attention mechanisms (introduced in "Attention is All You Need"), determines the variance of attention scores. This is mathematically analogous to the inverse temperature \( \beta \) in the Ising model, which governs the phase transitions of spin systems.
- If the traditional method of choosing \( \beta \) (introduced in "Attention is All You Need") is correct and optimal, it would imply that the authors of "Attention is All You Need" have effectively solved the N-dimensional Ising model by identifying its critical temperature through the standard deviation of all weights (i.e., the components of vectors in a spin-glass system).
But could this really be true? If the N-dimensional Ising model, a longstanding open problem in statistical mechanics, has not been solved, then does this suggest the traditional scaling factor \( \beta = \frac{1}{\sqrt{d_k}} \) might be suboptimal or oversimplified? Could dynamic optimization of β, as proposed in my work, offer a better approximation for the true critical behavior of these systems?
This reasoning employs proof by contradiction. By challenging the solution proposed in Attention is All You Need using the standard deviation of weights, i.e., parameters, for determining \( \beta \), and examining its equivalence to the critical temperature in the Ising model, I question whether the traditional scaling factor truly captures the underlying dynamics of transformer architectures and provides the solution to N-dimensional Ising-like models. I invite the community of academia, LLMs, and machine learning to further study this connection/similarity/equivalence and use it—and the well-established mathematics behind it—to determine the hyperparameters of LLMs.
Supporting Visuals

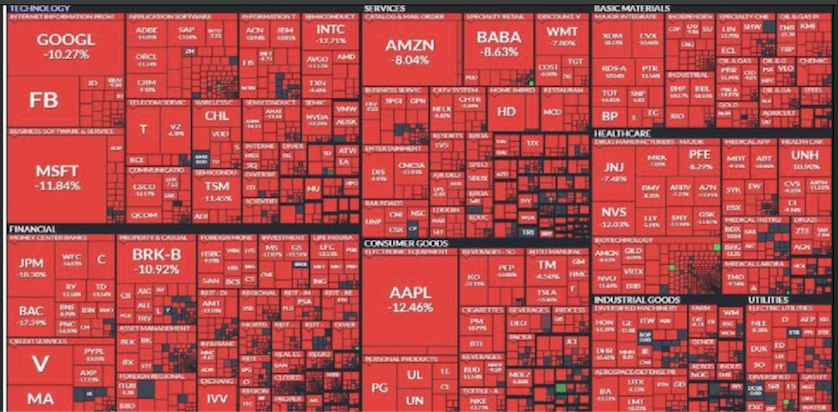
How My Research Could Have Prevented the $2 Trillion Market Evaporation
The Problem:
On January 27, 2025, U.S. markets lost $2 trillion in value due to the emergence of cost-efficient AI models like DeepSeek R1, developed by a Chinese AI startup. DeepSeek claimed to have built a large language model rivaling GPT-4 at a fraction of the cost, leveraging extreme efficiency and open-source access. This disruption highlighted vulnerabilities in the U.S. AI ecosystem, which relies heavily on brute computational power and proprietary, high-cost approaches.
How My Work Could Have Helped:
-
Cost-Efficiency Leadership:
- My research on dynamically optimizing the scaling factor \(\beta\) addresses the inefficiencies that made U.S. companies vulnerable to DeepSeek's disruption.
- By significantly improving transformer efficiency, my approach could have reduced the training costs of models like GPT-4, allowing U.S. companies to compete on cost with DeepSeek.
-
Early Adoption by U.S. Companies:
- If my work had been published on arXiv earlier and adopted by companies like NVIDIA or OpenAI, they could have implemented cost-saving measures to preempt DeepSeek's advantage.
- This would have demonstrated U.S. leadership in AI efficiency, reducing the market shock caused by DeepSeek's announcement.
-
Strengthening U.S. AI Leadership:
- My work offers a paradigm shift from brute computational scaling to intelligent optimization, positioning U.S. companies to lead the AI industry in both performance and cost-efficiency.
- Early integration of my methods into U.S. models would have preserved investor confidence in U.S. tech companies, preventing the massive market correction.
-
National and Economic Security:
- My results could have been framed as part of a broader strategy to secure U.S. leadership in AI, reducing the risk of economic shocks caused by foreign competition.
- By highlighting the strategic importance of efficiency-focused AI research, my work could have attracted government and industry support, ensuring its timely implementation.
Published Results
The key results from my work are summarized in the following table:
| Scaling Factor | Accuracy (%) | Observations |
|---|---|---|
| \(\beta = \frac{1}{\sqrt{d_k}}\) ~0.25 |
1.50 | Traditional method |
| \(\beta_{\text{opt}} = 6.67\) | 96.48 | Dynamic method |
Future Directions
Future work should extend this approach to diverse, real-world tasks, such as language modeling, machine translation, and computer vision. Second, the n-nary search algorithm, though effective, introduces computational overhead, which may be prohibitive for large-scale models. Developing more efficient algorithms for dynamically estimating \(\beta_{\text{opt}}\) is an important area for future research. Lastly, the interaction between \(\beta\) and other critical hyperparameters, such as learning rate, weight initialization, and attention head configurations, remains underexplored. A more comprehensive understanding of these interactions could lead to more holistic approaches to hyperparameter optimization.
My research from September 2023 demonstrated the necessity of examining all other hyperparameters to uncover potential redundancies in transformer architectures. By employing concepts from the Ising model (spin-lattice, i.e., quantized), it becomes possible to compress or distill models further by quantizing parameter values. Parameters that are zeroed out through this approach reveal redundancy within the model. This insight suggests that the quantization process, informed by spin-lattice physics, could be a key tool for improving model efficiency and scalability.
Furthermore, the algorithm I proposed for dynamically estimating \(\beta_{\text{opt}}\) can be translated into a reinforcement training framework. In this context, the algorithm adapts \(\beta\) in response to model feedback, effectively treating the optimization of \(\beta\) as a reinforcement learning problem. By iteratively refining \(\beta_{\text{opt}}\) based on real-time performance metrics, the algorithm could enable more adaptive, task-specific training. This approach not only enhances model efficiency but also provides a pathway for integrating reinforcement training principles into hyperparameter optimization.
Theoretical and Strategic Implications of My Research
1. Challenging the Mainstream Perspective: "Attention is All You Need"
The widespread adoption of the scaling factor \( \beta = \frac{1}{\sqrt{d_k}} \) in transformer-based architectures, as introduced by Vaswani et al. (2017) in "Attention is All You Need," lacks rigorous theoretical justification in modern large-scale implementations. This heuristic, though convenient, assumes that the variance of the attention score matrix remains constant during training—a simplification that breaks down as models scale and undergo dynamic updates.
Insisting on this traditional approach without revisiting its mathematical foundation essentially encourages researchers and industry leaders to take shortcuts—not in the sense of reducing training cost or improving theoretical development, but in prioritizing rapid implementation and commercialization over fundamental scientific rigor. By rushing to deploy models and bring AI products to market, mainstream researchers neglect deeper structural insights, leading to suboptimal architectures that persist due to inertia in the field.
The implications are profound: adhering to outdated methods risks stagnation in the field, perpetuating inefficiencies and hindering progress. My research not only addresses this gap but also paves the way for a principled re-evaluation of foundational assumptions in transformer architectures.
2. Strategic Implications of DeepSeek's Efficiency
The emergence of cost-efficient AI models, such as DeepSeek R1 developed by a Chinese startup, underscores the strategic vulnerabilities inherent in the U.S. AI ecosystem. By leveraging extreme efficiency, DeepSeek has demonstrated the capability to rival state-of-the-art models like GPT-4 at a fraction of the cost. This development is not merely a technological achievement but a potential game-changer in geopolitics and economic security.
If the PRC employs such advancements to iteratively improve their AI models and subsequently use those models to optimize semiconductor design and manufacturing, the implications are alarming. The current restrictions on NVIDIA, TSMC, and other chip manufacturers would become significantly less effective. Enhanced AI models could drive innovations in chip architecture, fabrication techniques, and supply chain efficiency, enabling the PRC to circumvent traditional dependencies on U.S. and allied technologies.
My research offers a counter-strategy by emphasizing efficiency and cost reduction in transformer architectures. By adopting dynamic scaling methods, U.S. companies can maintain a competitive edge, mitigating the risk of market disruptions caused by foreign competitors. Furthermore, integrating my methods into U.S. AI and semiconductor strategies would reinforce national security, ensuring leadership in critical technologies.
3. Strategic Countermeasures: Ensuring U.S. AI and Semiconductor Superiority
To counter the potential developments enabled by PRC’s AI-driven semiconductor advancements, proactive solutions must be implemented. Below are two publicly discussable strategies that can be disclosed without reliance on compartmentalized measures, ensuring operational security while mitigating the risk of unauthorized interception:
Solution 1: Establishing AI-Empowered Semiconductor R&D Initiatives
The U.S. must invest heavily in AI-accelerated semiconductor research to preemptively outpace adversarial developments. This includes:
- Integrating AI-driven chip design optimization using dynamic scaling factors to enhance efficiency and reduce costs.
- Funding collaborative research efforts between national labs, defense contractors, and academic institutions to develop secure, energy-efficient AI chips.
- Leveraging my research on transformer scaling factors to fine-tune AI-based chip architecture for superior performance.
Solution 2: AI-Optimized Export Controls and Supply Chain Resilience
Traditional export control mechanisms are becoming less effective in a world where AI can independently design optimized chips. Instead, the U.S. must:
- Implement AI-driven monitoring systems to track semiconductor supply chains and detect unauthorized technology transfers.
- Develop reinforcement-learning-based dynamic trade policies that adapt in real-time to counteract PRC's AI-driven semiconductor progress.
- Ensure that any AI model used in high-security domains incorporates dynamic security protocols to prevent adversarial exploitation.
These countermeasures are essential to ensuring that U.S. advancements in AI and semiconductor technologies remain strategically dominant. By integrating adaptive scaling techniques into AI-driven semiconductor R&D and export control strategies, the U.S. can effectively neutralize emerging threats and maintain technological superiority.
Distinguishing My Approach from OpenAI and DeepSeek
While organizations such as OpenAI and emerging competitors like DeepSeek have made significant strides in developing large language models (LLMs), their methodologies fundamentally differ from my research. My approach is rooted in a rigorous theoretical framework that identifies intrinsic values and redundancies within model parameters and hyperparameters. This foundational understanding not only explains why DeepSeek's distillation methods can achieve impressive results but also offers a more efficient and principled pathway to training highly capable models.
DeepSeek's method leverages the presence of redundant parameters—a phenomenon my research has elucidated as stemming from intrinsic values determined by the model's topology. By recognizing that a substantial portion of parameters do not contribute meaningfully to the model's performance, DeepSeek effectively reduces model complexity through distillation. However, this approach requires starting with a pre-trained model, which inherently involves significant computational resources and time. Moreover, distillation methods may inadvertently raise concerns about intellectual property, as they often necessitate access to the trained model's internal parameters.
In contrast, my research introduces a dynamic optimization framework that proactively identifies and eliminates these redundancies during the early stages of training—typically within the first few epochs. By optimizing hyperparameters such as the scaling factor \(\beta\) based on the model's topology, my approach ensures that only the most essential parameters are retained from the outset. This method drastically reduces the need for extensive training data and computational power. Empirical evidence from my studies demonstrates that optimizing a single hyperparameter can uncover significant redundancies, achieving accuracies ranging from approximately 1% to 97-100% using only 20% or less of the training data.
Furthermore, my approach addresses a critical limitation in mainstream methods, including those employed by OpenAI's ChatGPT, which typically operate under the assumption that intrinsic hyperparameter values are unknown or that dynamic optimization techniques to approximate these values are not feasible. This leads to a reliance on exhaustive hyperparameter searches and large-scale data requirements, which are both time-consuming and resource-intensive.
By leveraging a theoretically grounded method to ascertain intrinsic hyperparameter values dynamically, my approach eliminates the need for post-training distillation. This not only streamlines the training process but also avoids potential legal and ethical issues related to model distillation from proprietary APIs like OpenAI's. Additionally, optimizing all hyperparameters early on and dynamically zeroing out redundant parameters (akin to quantization with specific value gaps) paves the way for training models with significantly fewer parameters and less data, without compromising—and indeed enhancing—model performance.
The intrinsic value of hyperparameters such as \(\beta\) is predominantly determined by the model's topology, including factors like the number of connections each node possesses. This contrasts sharply with DeepSeek's distillation methods, which lack insight into these intrinsic values and thus rely on heuristics and post-hoc adjustments. My method provides a principled way to determine these values from the outset, ensuring that the model is both efficient and effective without the need for later modifications.
Moreover, if optimizing a single hyperparameter can reveal and eliminate large redundancies, it is reasonable to assert that a comprehensive optimization of all hyperparameters in the early stages of training could yield even more substantial improvements. Such an approach would enable models to achieve near-perfect accuracy with significantly less data by systematically identifying and zeroing out redundant parameters. This represents a paradigm shift in AI model training, moving towards more intelligent and efficient processes that are both data and computation-efficient.
In summary, my research not only provides a deeper theoretical understanding of parameter and hyperparameter redundancies but also offers practical solutions that surpass existing methods. By dynamically optimizing hyperparameters based on model topology early in the training process, my approach ensures that models are both highly efficient and capable, setting a new standard in the field of machine learning.